El teorema de Bayes es una herramienta fundamental en la Estadística. Dicho teorema fue descubierto por Thomas Bayes (1702-1761).
El Teorema de Bayes o probabilidad bayesiana es una de las diferentes interpretaciones de la probabilidad.
El Teorema de Bayes parte de una situación en la que se da la posibilidad de conocer la probabilidad de que ocurra una serie de sucesos Ai. En dicha probabilidad aparece un suceso B cuya ocurrencia proporciona cierta información, ya que una depende de la otra.
Las estadísticas bayesianas han intervenido de forma trascendente en distintos aspectos de la Física, con interpretaciones bayesianas de la mecánica cuántica y en las teorías de cuerdas y multiverso- hasta la investigación del cáncer, pasando por la ecología, la filosofía, la neurología, la psicología, además de la informática.
Hay hasta científicos cognitivos que han conjeturado que nuestros cerebros incorporan algoritmos bayesianos al percibir, deliberar y decidir, y fanáticos del teorema que señalan que si adoptáramos el razonamiento bayesianos de forma consciente, el mundo funcionaría bastante mejor.
Teorema de Bayes Fórmula
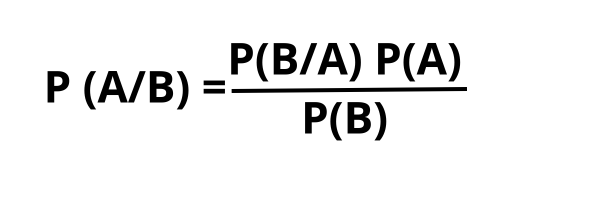
Teorema de Bayes ejercicios
Ejercicio 1. (Selectividad Andalucía MAT. CCSSII 2022)
El porcentaje de conductores que consumen alcohol durante la madrugada del sábado es del 5%. La policía
realiza controles de alcoholemia mediante un test del que se sabe que da positivo en un 96% si la persona ha
bebido alcohol y en un 10% si la persona no ha bebido alcohol.
Elegido al azar un conductor en la madrugada del sábado y realizado este test de alcoholemia, halle la probabilidad de que:
a) Si el test da positivo, el conductor haya consumido alcohol. (Sol. 0,3356)
b) El test dé negativo y el conductor no haya consumido alcohol. (Sol. 0,855)
c) Si el test ha dado negativo, el conductor no haya consumido alcohol. (Sol. 0,9976)
Ejercicio 2 (Selectividad Andalucía MAT. CCSSII 2023)
Disponemos de una moneda trucada en la que la probabilidad de obtener cara, al lanzarla, es el
doble de la de obtener cruz.
a) Halle la probabilidad de que, al lanzar la moneda, se obtenga cara. (Sol. 2/3)
b) Halle la probabilidad de que, al lanzar dos veces la moneda, se obtenga una cara y una cruz
sin importar el orden. (Sol. 4/9)
c) Halle la probabilidad de que, al lanzar dos veces la moneda, se obtenga al menos una cara. (Sol. 8/9)
d) Si al lanzar la moneda dos veces observamos que ha salido al menos una cara, halle la probabilidad de que se obtengan dos caras. (Sol. 1/2)
Ejercicio 3 (Selectividad Andalucía MAT.CCSSII 2021)
Se desea probar la eficacia de dos tipos de vacunas, A y B, contra un virus determinado. Para ello, se seleccionan 5000 voluntarios sin anticuerpos para este virus, a los que se les administra una de las vacunas o un placebo, resultando que 3000 reciben la vacuna A, 1500la vacuna B y el resto el placebo. Se comprueba que el 90% de los vacunados con la A y el 95% de los vacunados con la B, generan anticuerpos, no generando anticuerpos los que han recibido el placebo. Se selecciona uno de esos voluntarios al azar.
a) ¿Cuál es la probabilidad de que haya generado anticuerpos?. (Sol. 0,825)
b) Si dicho voluntario no ha generado anticuerpos, ¿qué probabilidad hay de que se le haya
administrado placebo? (Sol. 0,571)
Ejercicio 4 (Selectividad Andalucía MAT.CCSSII 2021)
Una empresa dedicada a la fabricación de coches lanza al mercado un nuevo modelo que
fabrica en tres plantas diferentes, A, B y C La planta A produce el 45% de los vehículos, la
planta B el 21% y el resto los produce la planta C. Se ha detectado un defecto en la colocación
del airbag, que afecta al 1% de los coches procedentes de la planta A, al 3% de los procedentes
de la planta B y al 2% de los de la planta C. Se selecciona un coche al azar de este nuevo
modelo.
a) ¿Cuál es la probabilidad de que no sea defectuoso y proceda de la planta C?. (Sol. 0,3332).
b) Si el coche elegido no es defectuoso, ¿cuál es la probabilidad de que proceda de la planta A? (Sol. 0,4534).
Ejercicio 5
Una empresa realiza el 50% de sus operaciones en la Unión Europea, el 30% en América y el 20% en Asia. En la Unión Europea sufren un retraso del 10%, en América del 15% y en Asia del 25%. Si una operación ha sufrido retraso, halla la probabilidad de que haya sido realizada en la Unión Europea. (Sol. 0,34).
Teorema de Bayes aplicaciones en la vida cotidiana
El Teorema de Bayes, una herramienta fundamental en la teoría de la probabilidad y tiene diversas aplicaciones en campos tan variados como por ejemplo:
- Inteligencia artificial: siendo esencial en aplicaciones como clasificación de texto, filtrado de spam, sistemas de recomendación y aprendizaje supervisado. En particular, el clasificador bayesiano se utiliza para la categorización de datos, mientras que las redes Bayesianas modelan dependencias probabilísticas entre variables. Este teorema también tiene aplicaciones significativas en el diagnóstico médico, donde se emplea para calcular la probabilidad de una enfermedad dado el historial clínico y los resultados de pruebas. En resumen, el teorema de Bayes proporciona un marco probabilístico robusto que potencia algoritmos de inteligencia artificial, permitiéndoles realizar predicciones y tomar decisiones informadas en función de la evidencia disponible.
- Medicina: El teorema de Bayes tiene aplicaciones fundamentales en el ámbito médico, siendo una herramienta valiosa en el proceso de diagnóstico y toma de decisiones clínicas. En el diagnóstico, se utiliza para calcular la probabilidad de que un paciente tenga una enfermedad específica en función de información previa, como síntomas y resultados de pruebas. Permite ajustar las probabilidades a medida que se obtienen nuevos datos, mejorando la precisión y confiabilidad de las decisiones médicas. Además, en la evaluación de la efectividad de pruebas diagnósticas, el teorema de Bayes es esencial para interpretar resultados y ajustar la probabilidad de enfermedad en función de la sensibilidad y especificidad de las pruebas. Su aplicación en la medicina contribuye significativamente a la personalización de tratamientos y a la optimización de los recursos clínicos, mejorando la atención y el manejo de la salud de los pacientes.
- Ciencia de datos: el teorema de Bayes es esencial en la evaluación de la efectividad de pruebas y experimentos. Permite ajustar la probabilidad de que una hipótesis sea cierta en función de los resultados observados, facilitando la interpretación de los datos y la toma de decisiones basada en la evidencia.
- Industria: El teorema de Bayes desempeña un papel crucial en la industria, abordando una variedad de desafíos y optimizando procesos. En el ámbito del mantenimiento predictivo, se utiliza para evaluar la probabilidad de fallos en equipos, permitiendo una planificación eficiente de actividades de mantenimiento. En el control de calidad, el teorema de Bayes contribuye a la toma de decisiones informadas al evaluar la probabilidad de defectos en productos basándose en pruebas de calidad. Además, en áreas como la gestión de inventarios y la seguridad laboral, el teorema de Bayes se aplica para prever la demanda y evaluar riesgos, mejorando la eficiencia operativa y la seguridad en el trabajo. Su aplicación en la optimización de procesos, gestión de proyectos, detección de anomalías y cadena de suministro subraya su versatilidad, convirtiéndolo en una herramienta esencial para gestionar la incertidumbre y tomar decisiones fundamentadas en la industria.