La combinatoria busca, a partir de un conjunto finito de objetos, cuántas
agrupaciones hay que cumplan ciertas condiciones. Lo dividiremos en 3 apartados:
Variaciones (importa el orden)
A. Con repetición
Son los casos en los cuales tenemos m elementos distribuidos en n agrupaciones
repetidas. Estas son las variaciones con repetición de m elementos escogidos n a n.
Son designados como:

➔ EJEMPLO:
¿Cuántos números de 3 cifras se pueden formar con los números 1, 2, 3, 4 y 5?
Como tenemos 5 elementos, que son los 5 números, y debemos de elegir 3 de esos
números para formar los números de 3 cifras:
𝑚 = 5 𝑛 = 3
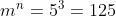
B. Ordinarias
Son los casos en los cuales tenemos m elementos distribuidos en n agrupaciones, los
cuales no se pueden repetir. Estas son las variaciones ordinarias, con repetición de
m elementos escogidos n a n. Son designados como:

⇑
(n factores decrecientes)
➔ EJEMPLO:
¿De cuántas formas se pueden repartir las 3 medallas a los 8 finalistas de una
carrera?
Disponemos de 8 elementos y hemos de clasificar ordenadamente a 3 de ellos. Para
el 1º , hay 8 posibilidades, para el 2º hay 7 posibilidades y para el 3º hay 6
posibilidades. Por lo tanto el número de posibilidades es:
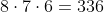
Permutaciones (importa el orden)
Las permutaciones son las distintas formas de las que se pueden ordenar los m elementos de un conjunto. Se designa como Pm ( “permutaciones de m elementos” ).

➔ EJEMPLO: ¿De cuántas formas pueden quedar clasificados los 5 participantes de un torneo?
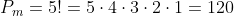
Combinaciones (No importa el orden)
Las combinaciones son las distintas agrupaciones que podemos formar tomando n elementos de un conjunto de m elementos, sin que importe el orden. Su fórmula se designa como:
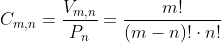
➔ EJEMPLO: En un grupo de 10 personas ¿de cuántas formas se pueden elegir a los 3 ganadores de un sorteo aleatorio? Como no influye el orden el orden de los ganadores del sorteo y los premios son iguales, el número de posibles elecciones es:
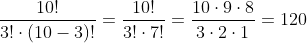
Ejercicios
Os dejamos este esquema resumen para que os sea más fácil entender la combinatoria y un par de ejercicios para que practiquéis:
1.-Se juegan 2 partidos. ¿Cuántas quinielas hemos de hacer para acertar los dos?¿Y para acertar 4 partidos? SOLUCIÓN: a)9 b)81
2.- ¿De cuántas formas pueden obtener los puestos 1º y 2º los 4 participantes en un torneo? SOLUCIÓN: 12
3.- Si tenemos 8 concursantes, ¿de cuántas formas podrían quedar clasificados entre ellos? SOLUCIÓN: 40320
4.- ¿Cuántos partidos han de jugar 4 amigos si deciden enfrentarse cada uno contra todos los demás? SOLUCIÓN: 6
5.- ¿Cuántos apretones de manos se darán 10 amigos que se encuentran? SOLUCIÓN: 45

Números combinatorios
A partir de las combinaciones se originan los números combinatorios:
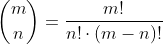

Triángulo de Tartaglia o de Pascal
Los números combinatorios originan el triángulo de tartaglia que se crea de la siguiente forma:
El triángulo de tartaglia tiene distintas propiedades:
- Los elementos de los extremos valen 1.
- En cada fila, los elementos simétricos son iguales.
- Cada elemento se obtiene sumando los dos que tiene encima.

Esperamos que os haya gustado nuestra entrada de Combinatoria

