Para qué sirve la Estadística

La estadística es una rama de las matemáticas que permite recopilar, organizar y analizar datos según sea necesario para obtener resultados, comparar información, tomar decisiones correctas, etc.

Normalmente, se dedica al estudio de una muestra o de una población con el objetivo de conseguir datos específicos. Además, puede emplearse para estudiar los problemas sociales, tomar decisiones, predecir el futuro y ofrecer soluciones eficaces en situaciones específicas. Esto se puede aplicar en diferentes ámbitos, como en la investigación científica y la medicina, que permite analizar los datos para validar y entender los resultados experimentales, la economía y el comercio, para poder realizar análisis de mercado, etc.

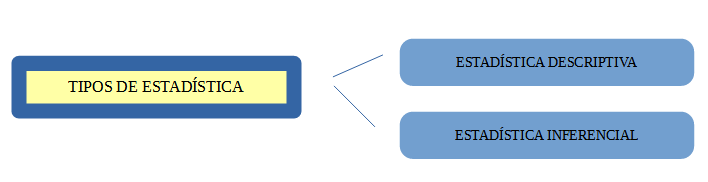
Tipos de Estadística

Estadística descriptiva

La estadística descriptiva es una de las ramas de la estadística que sintetiza los datos obtenidos para poder describirlos de forma medible y analizarlos, manteniendo las características específicas de esos datos. Para ello, se resume la información que se ha obtenido mediante una población o un grupo bajo una situación específica. Los estudios generados se representan a través de gráficos, que son una parte importante en el análisis de datos cuantitativos.

Se emplea en diferentes ámbitos, como en análisis de mercado, la logística, sistemas de control de calidad donde no es necesario hacer inferencias, etc.

Ejemplo de Estadística descriptiva

Un restaurante quiere ampliar su menú. Para ello, decide incluir opciones vegetarianas. Tras un tiempo, muchos restaurantes de la zona han empezado a introducir esta alternativa. Ante esto, el restaurante comienza a dudar sobre la rentabilidad de la inversión debido a la fuerte competencia.

Por este motivo, el restaurante, mediante análisis y encuestas por correo, recoge un conjunto de datos, representados en una gráfica, los cuales podrá analizar y reconocer patrones y tendencias.

Tipos de estadística descriptiva

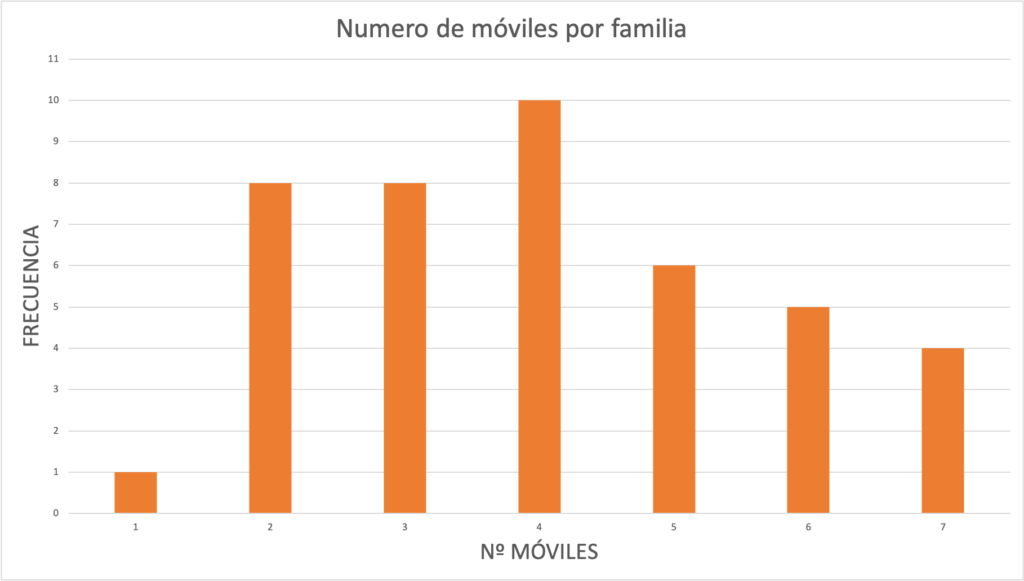
• Distribución de frecuencias

Describe la frecuencia con la que aparece cada resultado en un conjunto de datos o muestras. Normalmente, se representa en una tabla o un gráfico.

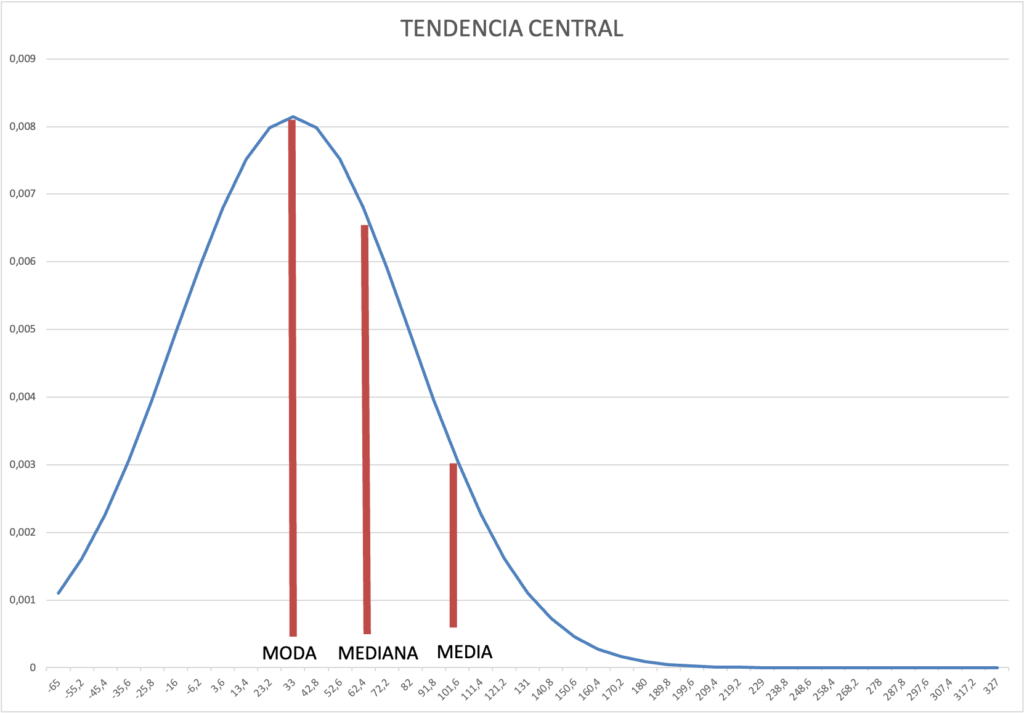
• Tendencia central

Consiste en un resumen descriptivo de un conjunto de datos empleando solo un valor el cual representa el centro de la distribución de los datos. Sus medidas son: la media, la mediana y la moda.

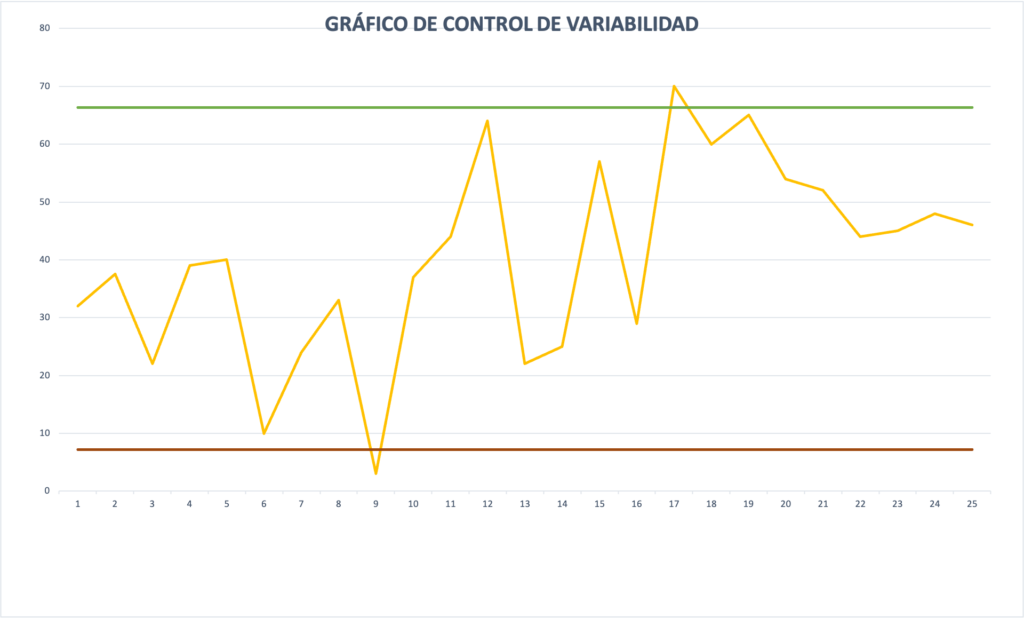
• Variabilidad

Indica que tan dispersos están los valores de un conjunto de datos. Si tiene una variabilidad alta, los datos se encuentras más esparcidos, en cambio, si tiene una variabilidad baja, los datos se encuentran más cercanos unos a otros. Las medidas de variabilidad comunes son: la varianza, la desviación estándar y el rango intercuartílico.

Estadística inferencial

La estadística inferencial es una rama de la estadística que se centra en hacer predicciones y conclusiones generalizadas, sobre características o comportamientos de una población más amplia, a partir de una muestra de datos de una población seleccionada.

Se suele utilizar en diferentes ámbitos, como en el análisis de mercado, sondeos hechos durante las elecciones parlamentarias, predicciones del tiempo, etc.

Ejemplo de estadística inferencial

Un colegio quiere averiguar cuál es mejor método de aprendizaje para medir el rendimiento escolar. Para ello, selecciona 3 clases aleatorias, A, B y C. Al curso A le asigna el método de exámenes, al B le asigna el de proyectos de investigación y al C el método de evaluación continua.

Durante todo el año escolar, el instituto reúne datos de las tres clases el cual les dará la información necesaria sobre las preferencias de esos alumnos. A partir de esas conclusiones, el instituto decidirá cuál es el mejor método de aprendizaje para medir el progreso escolar.

Dentro de la inferencial se encuentran los siguientes tipos:

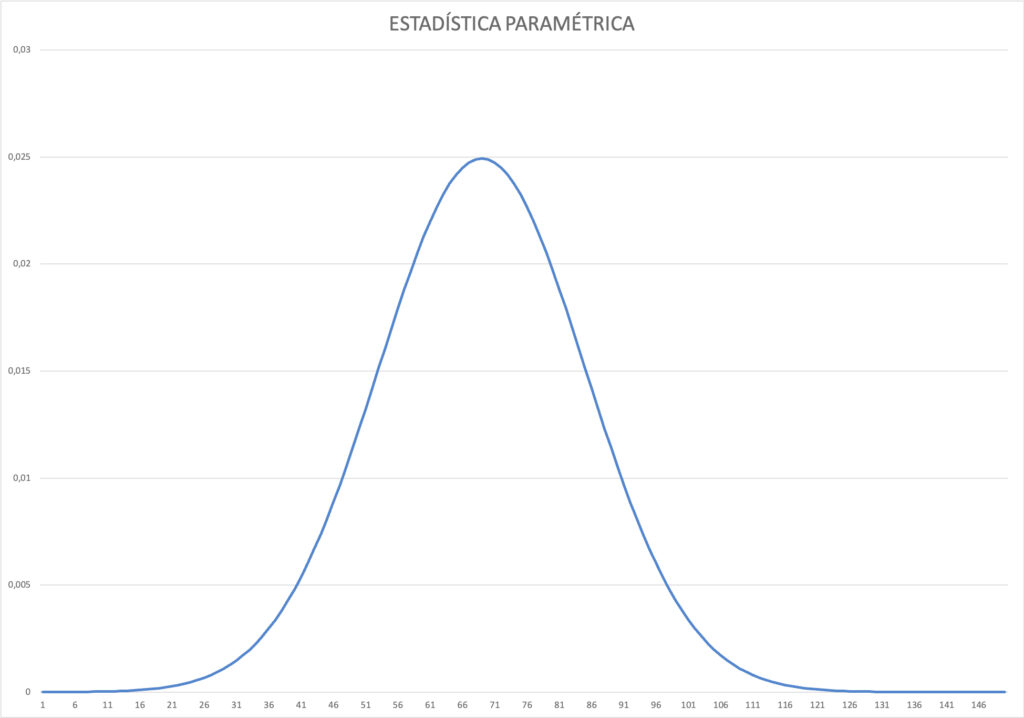
– Estadística paramétrica: se basa en supuestos de distribución de la población que tienden a ser normales, tendrá más exactitud y será más confiable.

Este enfoque se caracteriza por asumir la forma que poseen y los parámetros que van a tener nuestros datos. Esto nos permite utilizar herramientas estadísticas que sabemos a priori que funcionan bien con nuestra suposición.

Ejemplo de Estadística paramétrica

Vamos a suponer que nuestros datos tienen una forma de campana, como una campana normal. Sabiendo esto, utilizaremos métodos que funcionan bien cuando los datos se encuentran de esa forma.

Estadística no paramétrica: son las pruebas que no admiten una distribución de probabilidad para los datos y que requieren de menos supuestos. Se ocupa de analizar los datos que no siguen distribución particular. Se basan en hipótesis, en donde los datos no se encuentran distribuidos de forma normal.

Ejemplo de Estadística no paramétrica

Un centro de estudiantil quiere comparar cual método de estudio es mejor para la preparación de exámenes, A o B. No saben si las calificaciones tienen una distribución normal, por lo que deciden emplear la estadística no paramétrica para analizar los datos de ambos grupos.

Primero plantean dos tipos de hipótesis:

• No hay una diferencia importante en los resultados entre los grupos A y B.
• Hay una diferencia importante en los resultados entre los grupos A y B.

Para averiguar cuál método de estudio es mejor, utilizan la prueba de U de Mann-Whitney, la cual compara la suma de los rangos entre los dos grupos para averiguar el mejor método.

Usos de la Estadística

Como ya sabemos la estadística es una rama matemática que avanza día a día. En esta parte vamos a explicar diferentes aplicaciones tanto en el ámbito profesional como en el doméstico para ver para qué sirve la Estadística.

La Estadística en el ámbito profesional

En cuanto al ámbito profesional en los negocios, la estadística te permitirá conocer dónde se ubica la empresa, hacía dónde se dirige y qué acciones ha de tomar para lograr cumplir metas y objetivos. También permite hacer proyecciones a futuro para trabajar en proyectos que impulsen el crecimiento.

En cuanto al ámbito de la medicina la estadística se encargaría de recopilar y generar datos confiables de salud poblacional para la toma de decisiones como podría ser recopilar síntomas de varios pacientes y enlazarlos a cualquier enfermedad.

La Estadística en el ámbito doméstico

En la vida cotidiana la estadística tiene muchísimas utilidades que nos rodean sin darnos cuenta, por ejemplo, las plataformas con contenidos visuales (Netflix, HBO, Prime Video…) utilizan la estadística para recomendarnos contenido dependiendo de nuestros gustos y preferencias.

Otro ejemplo más diario podría ser cuando compramos en el supermercado acorde a los gustos de nuestros familiares (comprar menos verdura si a mi padre no le gusta).

La Estadística en la Economía

En economía, la estadística se utiliza para analizar tendencias económicas, evaluar el rendimiento financiero, pronosticar cambios en los mercados y tomar decisiones en política económica.

La Estadística en la Medicina

En medicina, la estadística se aplica para analizar ensayos clínicos, evaluar la eficacia de tratamientos, estudiar la prevalencia de enfermedades y analizar datos epidemiológicos.

Esperamos que os haya gustado esta entrada en la que hemos explicado para qué sirve la Estadística