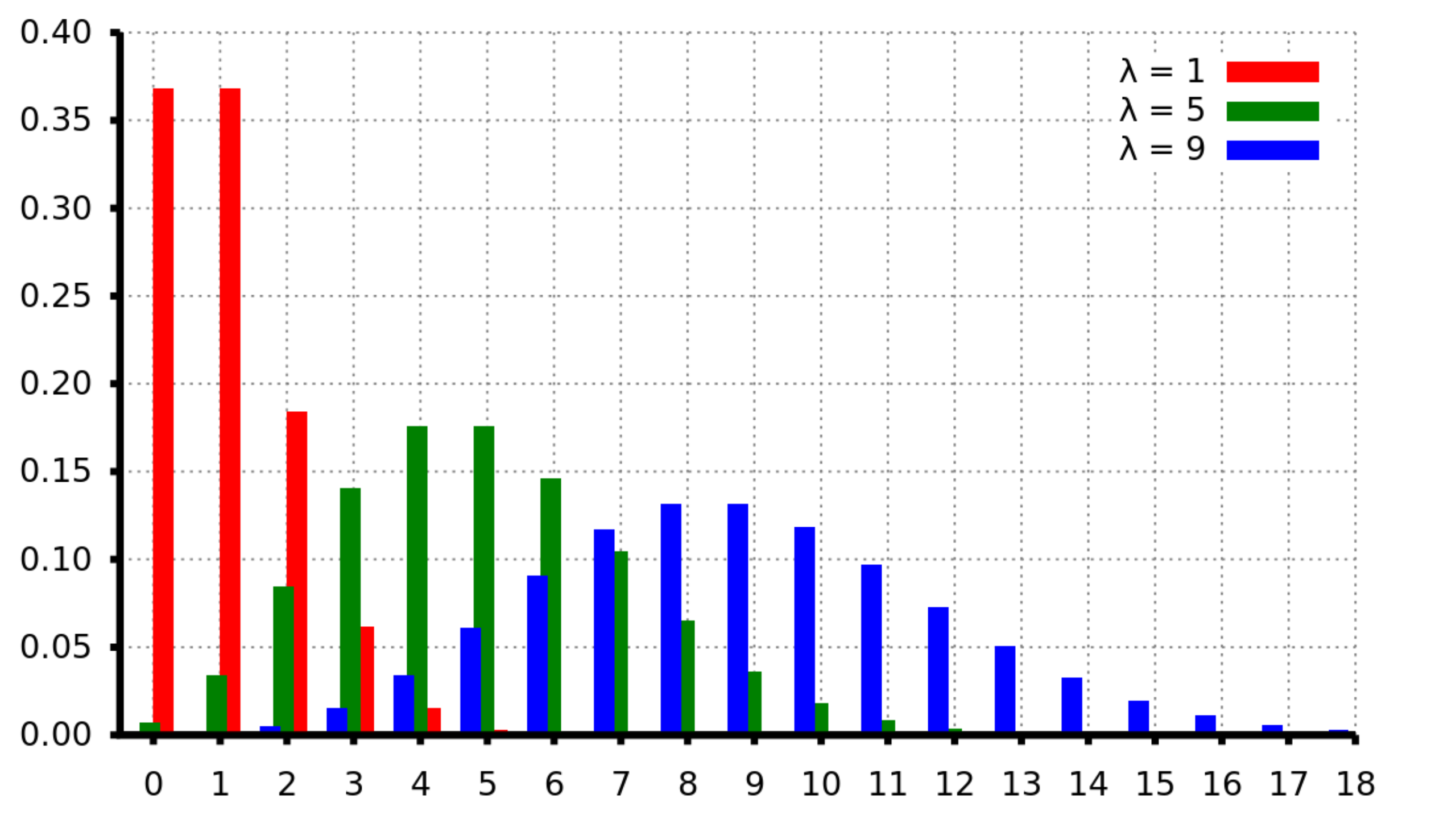
La Ley de Poisson o Distribución de Poisson es una de las distribuciones de variable discreta más importantes. Nos proporciona la probabilidad que ocurra un suceso un número x de veces. Esta ley fue propuesta por Simeón Poisson en 1837.
La Distribución de Poisson se da en situaciones en que tenemos un gran número de experimentos independientes y una pequeña probabilidad de éxito en cada uno de ellos, preguntándose cuál es la probabilidad de obtener x éxitos en n experimentos. Tiene como particularidad que su media y su varianza son iguales.
Ley de Poisson Fórmula
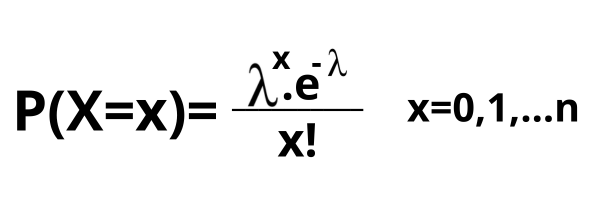
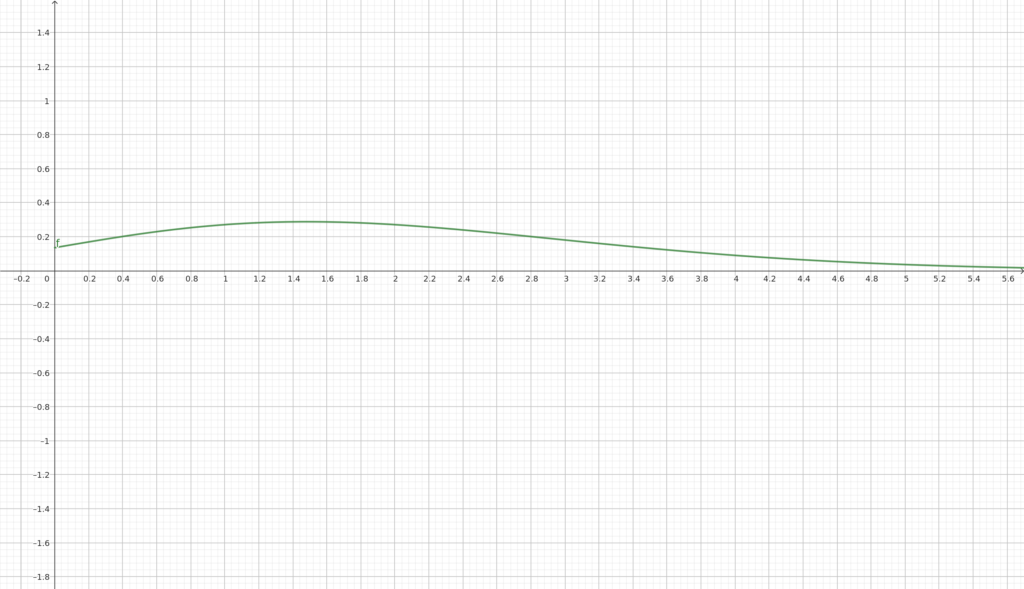
Gráfica de la Distribución de Poisson con media=2
Media y Varianza de una distribución de Poisson
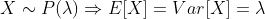
Distribución de Poisson ejemplos
1. El veterinario recibe al día de promedio 4 pacientes. Sabiendo que el número de pacientes que recibe al día sigue una distribución de Poisson. Calcula la probabilidad de que un día determinado lleguen 3 pacientes. (Solución: 0,1954).
2. Una compañía telefónica recibe llamadas a razón de 5 llamadas por minuto. Calcular la probabilidad de:
a) Recibir menos de 3 llamadas en un minuto. (Solución: 0,0825)
b) Recibir 3 llamadas en un minuto. (Solución: 0,14037)
c) No recibir ninguna llamada en un minuto.(Solución: 0,0067).
3. Si un banco recibe en promedio 8 cheques sin fondo por día, ¿cuál es la probabilidad de que reciba cuatro cheques sin fondo en un día dado?. (Solución: 0,0572).
4. Un médico recibe un promedio de 6 visitas al día. Sabiendo que el número de pacientes que llegan un día sigue una distribución de Poisson. Calcula la probabilidad de que lleguen 4 pacientes en un día. (Solución: 0,1338).

También podría interesarte…

Combinatoria
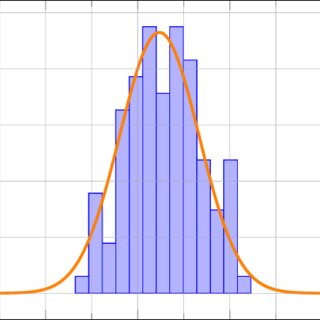
Curtosis.

Nota de Prensa