¿Qué es la ley de Benford?
La ley de Benford, también conocida como la ley del primer dígito, explica que, en ciertos campos del mundo real, con un conjunto de números muy grande, hay más probabilidad de que el primer dígito sea 1 a que sea cualquier otro, y esta probabilidad disminuye conforme aumenta el dígito.
Gráfica Ley de Benford
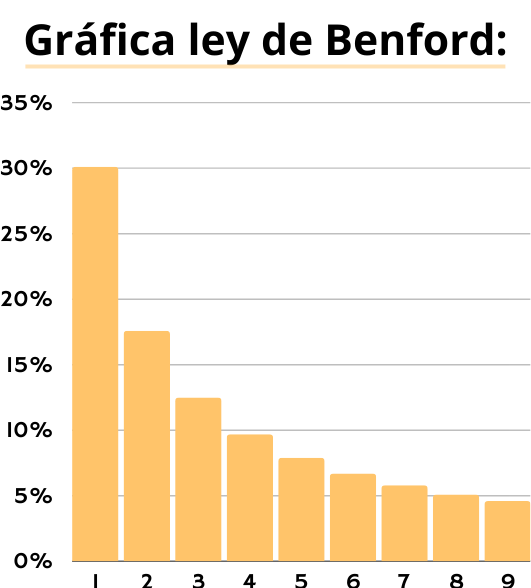
Esta gráfica representa la distribución de los primeros dígitos según la ley de Benford. Se describen en el eje X los números del 1 al 9 y en el eje Y los porcentajes de probabilidad de que aparezcan como primer dígito de un conjunto de números muy grande (en ciertos campos del mundo real). Podemos observar como esta probabilidad disminuye conforme el número es mayor. Notamos una notable diferencia entre el número 1 que tiene un 30.1% de probabilidad y por el otro lado, el número 9 que tiene tan solo un 4.6%.
¿Cómo se formó la Ley de Benford?
Pese a que la ley fue formulada finalmente por Frank Benford en 1938, se empezaron a dar evidencias de esta
misma desde el 1881 cuando el matemático y astrónomo Simon Newcomb observando tablas de logaritmos, se fijó en que determinadas paginas estaban más usadas que otras, pero este no formuló ninguna relación matemática.
Paralelamente, Benford se fijó en el mismo suceso y quiso ponerlo a prueba en otros ámbitos del mundo real, dándose cuenta de que esto se repetía en muchos casos, lo que lo llevó a formular lo que hoy se conoce como “La ley de Benford”.

Formulación matemática de la Ley de Benford
Esta ley establece que la probabilidad de que la primera cifra sea un determinado número es igual al logaritmo de dicho número más uno, menos logaritmo de dicho número, simplificado sería: logaritmo de uno más uno partido por dicho número.
Por lo que la fórmula de la ley de Benford es la siguiente:
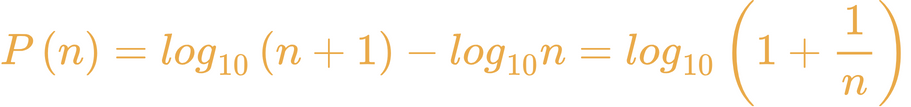
Aplicaciones de la Ley del primer dígito
La ley del primer dígito tiene distintas aplicaciones en muchos ámbitos del mundo real, como la genética, la economía o la política entre otras. Pero la más importante es:
Detección de fraudes por la Ley de Benford
Dado que dicha norma se cumple que en un conjunto de números muy grande, hay más probabilidad de que el primer dígito sea 1 a que sea cualquier otro, también debería cumplirse con los importes de cobros y pagos de una empresa, así lo supuso el Dr. Mark J. Nigrini de la Universidad de Kansas, que empezó a llevar a cabo investigaciones usando este principio matemático, consiguiendo rápidamente importantes resultados.
Debido a las investigaciones de todos estos científicos, la policía cuenta ahora con una nueva herramienta para detectar el fraude fiscal, con la que ya han conseguido detectar estafas en muchas empresas.
