Para calcular los intervalos de confianza para la media de población µ con un nivel de confianza 1-α tenemos que dominar las siguientes fórmulas:
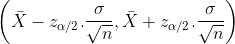
| Extremo inferior | |
| Extremo superior | |
| Amplitud del intervalo | |
| Error de la muestra |
Ejercicios de Intervalos de confianza para la media
1.El número de días de permanencia de los enfermos en un hospital sigue una ley Normal de media µ y desviación típica 3 días.
a) Determine un intervalo de confianza para estimar µ, a un nivel del 97%, con una muestra aleatoria de 100 enfermos cuya media es 8,1 días.
b) ¿Qué tamaño mínimo debe tener una muestra aleatoria para poder estimar µ con un error máximo de 1 día y un nivel de confianza del 92%?
Solución: a) (7,449;8,751) b) El tamaño de la muestra ha de ser, como mínimo de 28 enfermos.
2. Los directivos de una empresa desean estimar el tiempo medio que tardan los empleados en llegar al puesto de trabajo desde sus domicilios. Admitimos que dicho tiempo sigue una distribución Normal de desviación típica 8 minutos. Se elige al azar una muestra de 9 empleados de esa empresa, obteniéndose los siguientes resultados, expresados en minutos: 10, 17, 8, 27, 6, 9, 32, 5, 21
a) Determine un intervalo de confianza al 92%, para la media poblacional.
b) Con una confianza del 95’5%, ¿Qué tamaño muestral mínimo sería necesario para estimar el tiempo medio con un error inferior a 1’5 minutos?.
Solución: a)(10,32 ; 19,68) b) n=115
3. El tiempo (en horas) que permanecen los coches en una determinado taller de reparación es una variable con distribución Normal de desviación típica de 4 horas.
a) Se eligieron, al azar, 16 coches del taller y se comprobó que, entre todos, estuvieron 136 horas en reparación. Determine un intervalo de confianza, al 98,5%, para la media del tiempo que permanecen los coches en ese taller.
b) Determine el tamaño mínimo que debe tener una muestra que permita estimar la media del tiempo que permanecen en reparación los coches en ese taller con un error en la estimación no superior a una hora y media y con el mismo nivel de confianza del apartado anterior.
Solución a) (6,07;10,93) b) La muestra debe tener, como mínimo, un tamaño de 42 coches.
4. La cantidad de azúcar que añade un fabricante de refrescos a sus productos sigue una ley Normal cuya varianza es 225 mg2 . Se ha seleccionado al azar una muestra de 25 refrescos de ese fabricante, en la que se ha obtenido una media de 175 mg de azúcar añadido por refresco.
a) Determine un intervalo de confianza al 90% para la cantidad media de azúcar añadida a cada
refresco.
b) ¿Cuál debe ser el tamaño mínimo de la muestra para que el intervalo de confianza correspondiente al 80% tenga una amplitud como máximo de 5 mg?.
Solución: a) (170,065 ; 179,935) b) n=60 refrescos como mínimo.
5. De una población Normal de media desconocida µ y desviación típica 2 se extrae la siguiente muestra aleatoria simple de tamaño 10:
3’8 6’3 4’3 6 6’2 5’8 1’5 3’3 3’4 2’9
a) Estime, mediante un intervalo de confianza, la media poblacional para un nivel de confianza del 92%. Obtenga su error de estimación.
b) (1 punto) ¿Qué tamaño muestral mínimo sería necesario para reducir ese error a la mitad, con el mismo nivel de confianza?
Solución: a) media poblacional= 4,35; E=1,1068. b) n=40
6. De una población se sabe que el tiempo dedicado a ver la televisión sigue una distribución normal con desviación normal con desviación típica 42 minutos.
a) Se conoce que la media es de 175 minutos y se elige una muestra de 36 individuos de esa población. Determina la probabilidad de que el consumo medio de televisión entre los individuos de la muestra esté entre 165 y 180. (Solución=0,6848)
b) A diferencia del apartado anterior, desconocemos la media poblacional. Si la muestra de tamaño 36 arroja un consumo de 170 minutos, calcula el intervalo de confianza para la media poblacional con 95% de probabilidad. (Solución= (156.28;183.72)).
7. Un fabricante de tuberías PVC sabe que la distribución de los diámetros interiores de los tubos de conducción de agua que produce sigue una ley Normal con varianza de 0.25 mm². Para estimar el diámetro medio de esas tuberías, toma una muestra aleatoria de 64 tubos y comprueba que el diámetro medio de esa muestra es de 20 mm.
a) Calcule un intervalo de confianza, con un nivel del 98%, para la media de los diámetros de los tubos que fabrica. (Solución= (19.8543;20.1456)).
b) Halle el tamaño mínimo que debe tener una muestra de esa distribución para que la amplitud de un intervalo de confianza, con ese mismo nivel de confianza, sea inferior a 2 mm. (Solución al menos n=2 tubos).
8. El tiempo en horas dedicado cada día al uso de una aplicación de mensajería instantánea por
los estudiantes de bachillerato de una ciudad, es una variable aleatoria que sigue una ley
Normal con desviación típica 0.5 horas. Se toma una muestra aleatoria de 10 estudiantes y se
obtienen los siguientes tiempos de uso en horas:
3.5 4.25 2.25 3.75 4.2 2.75 1.25 1.2 1.75 2.1
a) Determine un intervalo de confianza al 90% para el tiempo medio diario dedicado al uso de
esta aplicación por los estudiantes. (Solución= (2.44; 2.96)).
b) Calcule el tamaño muestral mínimo necesario para estimar el tiempo medio diario dedicado
al uso de esta aplicación, para un error de estimación no superior a 0.1 horas y mismo nivel de
confianza anterior. (Solución: n=68).

Combinatoria
Curtosis.

Nota de Prensa

El mejor profe que jamás he tenido!!!!