La distribución normal fue descrita por el matemático alemán Carl Friedrich Gauss. Esta distribución, también conocida como la campana de Gauss, desempeña un papel central en la estadística y se encuentra en el corazón de numerosos fenómenos naturales y sociales. Se llama distribución normal porque aparece de forma muy habitual en la naturaleza, por ejemplo en estudio de notas medias o en las alturas de una población.
¿Qué es la distribución de Gauss y por qué es importante?
La Distribución Normal es un modelo matemático que describe la forma en que se distribuyen los datos en una población. Su característica distintiva es su forma de campana simétrica, con la media, mediana y moda ubicadas en el centro. Este patrón simétrico significa que la mitad de los datos se encuentran a cada lado de la media, creando una representación gráfica elegante y poderosa. Podríamos decir que es la distribución más común que podemos encontrar.
Gráfica de la Distribución Gaussiana
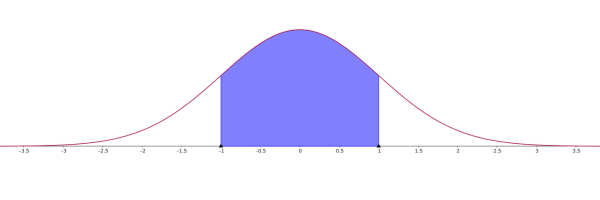
Distribución normal tipificada
La distribución normal tipificada tiene las siguientes características:
- Su media es 0.
- Su varianza es 1 y su desviación típica es 1.
- Su gráfica es simétrica respecto al Eje OY.
- Tiene 2 puntos de inflexión, uno en 1 y otro en -1.

Probabilidad de una distribución N(0,1)
- Caso k>0, P(Z<k)
- Caso k>0; P(Z>k)=1-P(Z<k)
- Caso k<0; P(Z<k)=1-P(Z<-k)
- Caso (k1<Z<k2)=P(Z<k2)-P(Z<k1)
La Regla del 68-95-99,7
Una de las características más poderosas de la Distribución Normal es la Regla 68-95-99.7. Esta regla establece que, en una distribución normal, aproximadamente el 68% de los datos caen dentro de una desviación estándar de la media, el 95% dentro de dos desviaciones estándar y el 99.7% dentro de tres desviaciones estándar. Esta propiedad facilita la interpretación y análisis de conjuntos de datos.
Ejercicios Distribución Normal
1.Sea Z una N(0,1), se piden las siguientes probabilidades:
a) P(Z<2,56)= (Solución=0,9948)
b) P(Z<-1,56)= (Solución=0,0594)
c) P(0,6<Z<2,05)= (Solución=0,254)
2. El salario de los jóvenes recién incorporados al mercado laboral sigue una distribución normal de media 900€ con una varianza de 4000. Se elige al azar a un joven, calcula la probabilidad de que cobre más de 1000€.
3. Calcula el intervalo característico de una N(0,1) correspondiente a una probabilidad de 0,95.
4. En una distribución N(110,10), calcula las siguientes probabilidades:
a) P(100<X<130)= (Solución 0,8185).
b) P(X>130)= (Solución 0,0228).
5. El número de kilómetros que puede circular un automóvil de una determinada marca en condiciones óptimas, sin realizar una revisión, sigue una distribución normal de media 35.000 kilómetros y desviación típica 4.000 kilómetros.
a) ¿Qué probabilidad de vehículos funcionará correctamente durante más de 38.000 kilómetros?. (Solución: 0,2266)
b) ¿Qué probabilidad de vehículos deberá ser revisado entre los 32.000 y 38.000 kilómetros?. (Sol: 0,5468).
Aplicaciones de la distribución Gaussiana
La Distribución Gaussiana o Normal se manifiesta en innumerables aspectos de la vida cotidiana. Desde la estatura de la población hasta las puntuaciones en exámenes, y desde la variabilidad en la producción industrial hasta las fluctuaciones del mercado financiero, la presencia de la Distribución Normal es omnipresente. Comprender sus principios permite realizar predicciones y tomar decisiones informadas en diversos campos.